Wahrscheinlichkeit: Das Rückgrat der künstlichen Intelligenz

Benötigte Lesezeit: 4 Minuten

Wie hoch ist die Wahrscheinlichkeit zweimal in Folge im Lotto zu gewinnen? Wie stehen die Chancen, dass es am 19. Oktober regnet? Werde ich heute zufällig einen Freund aus der Grundschule treffen? All diese Fragen sind schnell gestellt, aber gar nicht so einfach zu beantworten. Wahrscheinlichkeitsrechnung ermöglich uns die Berechnung der Chance, dass ein bestimmtes Ergebnis durch einen zufälligen Prozess zustande kommt. 

Wie das Wort “Rechnung” bereits sagt, werden mathematische Formeln verwendet, um möglichst genaue Wahrscheinlichkeiten zu kalkulieren. Die Grundlage dafür sind Daten, zum Beispiel über das Wetter am 19. Oktober in den letzten zehn Jahren. Sind diese Informationen verlässlich, ist auch das Ergebnis für den kommenden 19. Oktober zuverlässig. Die Qualität der Daten bestimmt also, wie gut eine Vorhersage ist.

Nehmen wir an, dass es am 19. Oktober mit 30-prozentiger Wahrscheinlichkeit regnet. Bedeutet dies, dass es an diesem Tag nicht regnet – da der Wert unter 50 Prozent liegt? Nicht unbedingt. Es ist unwahrscheinlich, aber nicht ausgeschlossen. In gewisser Weise, ist die Wahrscheinlichkeit also ein Maß für Unsicherheit. 

Wie hängen Wahrscheinlichkeitsrechnung und KI zusammen?

Vorhersagen sind das Brot und die Butter von maschinellem Lernen und KI. Das Ziel eines KI Modells besteht immer darin, eine Entscheidung zu treffen. Zeigt das Bild eine Katze oder einen Hund? Welcher nächste Zug ist am erfolgversprechendsten in einem Schachspiel? Welche Übersetzung für ein Wort ist die passendste, in einem spezifischen Satz oder Kontext?

Fragestellungen wie diese, werden beim maschinellen Lernen so modelliert, dass die Antwort eine Wahrscheinlichkeit ist. Im Falle einer Bildklassifizierung, funktioniert das zum Beispiel folgendermaßen: 

Tierbild => (Berechnung des Deep Learning Modells) => Ergebnis: [75% Hund, 20% Katze, 3% Delphin, 2% Fisch]

Dies kann in der Wahrscheinlichkeitsrechnung wie folgt umgeschrieben werden: P (C = Hund | Tierbild) = 0,75. 

Das Bild zeigt also mit 75%iger Wahrscheinlichkeit einen Hund. Im Falle eines Schachspiels, würden die “Überlegungen” eines Deep Learning Modells ähnlich lauten: Der erste mögliche Zug hat eine Erfolgswahrscheinlichkeit von 0,3 und die zweite Möglichkeit hat eine Erfolgswahrscheinlichkeit von 0,7. Anhand dieser Ergebnisse trifft der Computer dann eine Entscheidung und macht seinen Zug. 

Eine korrekte Antwort, kann nicht immer garantiert werden. In der Regel müssen KI-Modelle trainieren, um Fehlerquoten zu minimieren. Der statistische Charakter sowohl des Lernens als auch der Vorhersage bedeutet, dass alle derzeit in der Praxis befindlichen ML- und KI-Systeme probabilistisch sind.

Das liegt auch daran, dass Entscheidungen oft mit unvollständigen Informationen getroffen werden müssen. Dies erfordert einen Mechanismus zur Quantifizierung der Unsicherheit – den die Wahrscheinlichkeitsrechnung bietet. Mit ihrer Hilfe können unsichere Elemente – wie das Risiko bei Finanztransaktionen und vielen anderen Geschäftsprozessen – modelliert werden. 

Ein solides Verständnis der Wahrscheinlichkeitstheorie ist also unumgänglich, um maschinelles Lernen auf einer tieferenen Ebene zu verstehen. Es ist außerdem essentiell, um zu erkennen, welche Prozesse in einem Modell ablaufen, um Fehler zu erkennen und zu beheben.

Die Mathematik hinter der Wahrscheinlichkeitsrechnung

Eine Wahrscheinlichkeit wird mathematisch als “P” angegeben, abgeleitet von der englischen Übersetzung des Wortes – “Probability”. Sie wird definiert für ein Ereignis (Event) E. Die Wahrscheinlichkeit, dass Event E eintritt wird in Prozent gemessen und sieht in einer Formel dann so aus: P(E) = x%. 

Die Wahrscheinlichkeitstheorie beinhaltet vier wichtige Konzepte: 

1. Das Ereignis – ein Event, dem eine Wahrscheinlichkeit zugeordnet ist. 
2. Den Ergebnisraum (im Englischen = Sample Space), der die Menge der möglichen Ergebnisse für ein Event darstellt.
3. Die Wahrscheinlichkeitsfunktion (im Englischen = Probability Function), die einem Ereignis eine Wahrscheinlichkeit zuordnet. Die Wahrscheinlichkeitsfunktion gibt die Wahrscheinlichkeit an, dass das Ereignis Teil des Ergebnisraums ist. 
4. Die Wahrscheinlichkeitsverteilung (im Englischen = Probability Distribution) repräsentiert die Form oder Verteilung aller Ereignisse im Ergebnisraum. 

Die Wahrscheinlichkeit eines Events kann berechnet werden, indem alle Ereignisse eines Events gezählt und durch die Summe aller Vorkommnisse des Ereignisses dividiert werden. Die Wahrscheinlichkeit ist ein Bruchwert und hat einen Wert im Bereich zwischen 0 und 1, wobei 0 keine Wahrscheinlichkeit und 1 die volle Wahrscheinlichkeit darstellt.

Es gibt zwei Möglichkeiten, Wahrscheinlichkeit zu interpretieren: 

• Die frequentistische Wahrscheinlichkeit, welche die tatsächliche Wahrscheinlichkeit eines Ereignisses berücksichtigt. Sie basiert auf Zählungen oder Stichproben bestehender Daten.
• Die Bayes’sche Wahrscheinlichkeit berücksichtigt, wie stark wir annehmen, dass ein Ereignis eintreten wird. Sie basiert also auf Annahmen oder persönlichen Überzeugungen. Die Bayes’schen Techniken können verwendet werden, um Ereignisse zu modellieren, die zuvor nicht oder nur selten aufgetreten sind (wo also noch keine Daten existieren). 

Nun mag das bisher alles recht logisch klingen, doch die Mathematik hinter diesen Vorgängen ist komplex und kann schnell so aussehen:

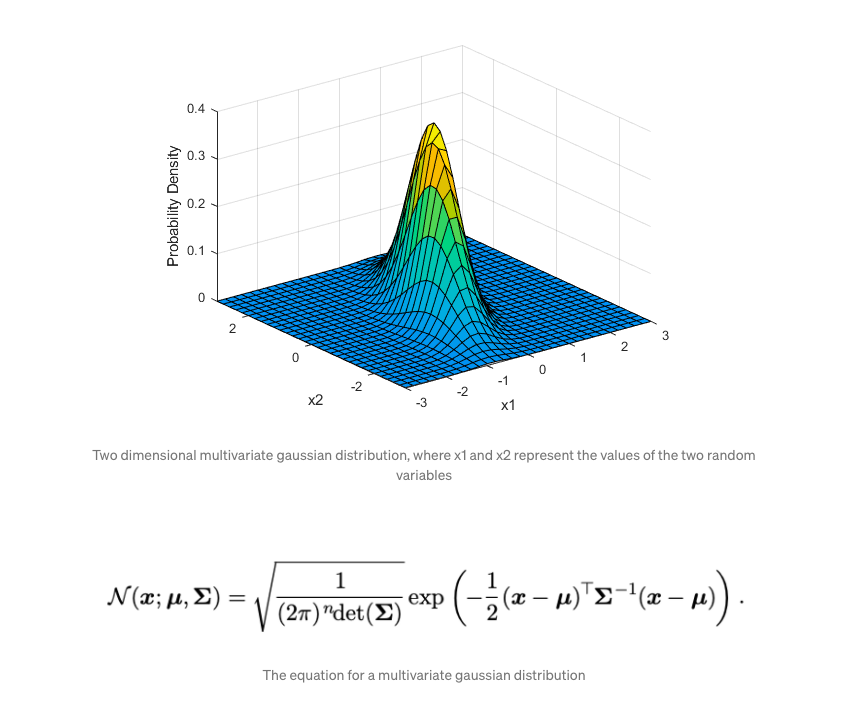
Glücklicherweise gibt es zahlreiche YouTube Videos und Online-Lehrgänge, die einem das Thema erklären, etwa bei Udemy oder wiwiweb.de. Wer sich mit den mathematischen Grundlagen sicher fühlt und fließend Englisch spricht, dem stehen zudem diverse Angebote internationaler Universitäten zur Verfügung.

Mein Fazit: Wahrscheinlichkeitsrechnung ist ein hochinteressantes, aber auch sehr komplexes, mathematisches Thema. Es ist zudem ein sehr weites Feld und nicht alle Elemente sind notwendig, um maschinelles Lernen in Tiefe zu verstehen. Wer KI und Wahrscheinlichkeitsrechnung in Kombination erlernen möchte, sollte sich daher gezielt nach spezifischen Kursen umschauen.

Quellen:

• https://www.quora.com/How-is-probability-related-to-machine-learning-and-AI
• https://medium.com/datadriveninvestor/all-the-probability-fundamentals-you-need-for-machine-learning-93a177dc9aea
• https://www.datasciencecentral.com/profiles/blogs/understanding-the-applications-of-probability-in-machine-learning

Bild: DALLE 2